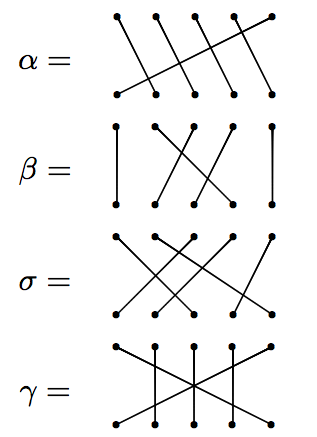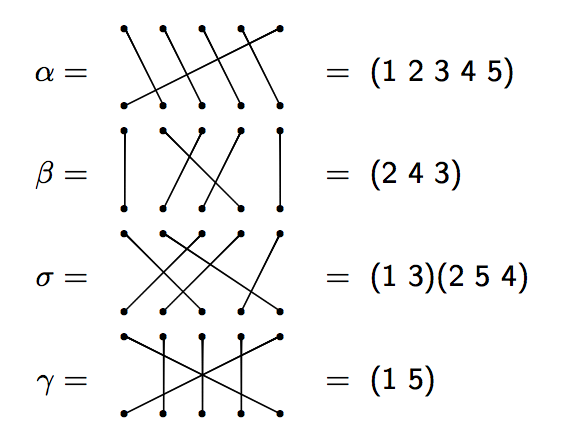Futurama
- Futurama is an American animated science fiction sitcom created by Matt Groening (of The Simpsons).
- The series aired on Fox from 1999-2003, and then began airing on Comedy Central in 2008. Season 7 coming in 2012.
- The show follows the adventures of a late 20th-century New York City pizza delivery boy, Philip J. Fry, who was accidentally frozen in 1999 and then thawed out on New Year's Eve 2999.
- Some main characters: Fry, Leela (one-eyed alien), Bender (robot), Professor Farnsworth (Fry's distant nephew and mad scientist), Zoiberg (lobster-like alien), Amy (spoiled and accident prone student), and more.
The Prisoner of Benda
- "The Prisoner of Benda" is episode 10 of season 6 and aired on August, 2010.
- The title is a play on "The Prisoner of Zenda", a 1894 novel by Anthony Hope Hawkins.
- In the episode, Farnsworth and Amy build a machine that allows them to switch minds. However, they learn that the machine cannot be used twice on the same pair of bodies. After several characters swap minds, the rest of the episode is focused on how to return everyone's minds back to their original owner.
- With the help of two Harlem Globetrotters (and some mathematics), the irreversible mind swap problem is solved.
- Episode written by Ken Keeler, who has a PhD in applied mathematics from Harvard.
- Keeler invented and proved a mathematical theorem specifically for the show.
The mind swap problem
Here are the swaps that take place during the episode:
- Professor ($p$) $\leftrightarrow$ Amy ($a$)
- Amy ($a$) $\leftrightarrow$ Bender ($b$)
- Professor ($p$) $\leftrightarrow$ Leela ($l$)
- Amy ($a$) $\leftrightarrow$ Wash Bucket ($w$)
- Fry ($f$) $\leftrightarrow$ Zoiberg ($z$)
- Emperor Nikolai ($e$) $\leftrightarrow$ Wash Bucket ($w$)
- Hermes($h$)$\leftrightarrow$ Leela ($l$)
The upshot:
\[a \rightarrow h \rightarrow l \rightarrow p \rightarrow b \rightarrow e \rightarrow w \rightarrow a \text{ and } f \leftrightarrow z\]
The mind swap problem (continued)
The question is:
Can the machine be used to put everyone's mind back in the proper body if we are not allowed to use the machine on the same pair of bodies more than once?
We need to use math!
The symmetric group
We can model this problem in terms of permutations (i.e., rearrangements) of numbers. It turns out that the set of all permutations of the numbers 1 through $n$ forms a "group" under composition.
A group is a set with an associative binary operation satisfying:
closure:
the "product" of any two elements from the set is an element of the set.identity:
there exists a "do nothing" element.inverses:
for every element in the set, there exists another element in the set that "undoes" the original.
The group of permutations of $\{1,2,\ldots, n\}$ is called the symmetric group and is denoted by $S_n$.
Permutation diagrams
One way of representing an element of the symmetric group is via permutation diagrams, which we illustrate by way of example.
Example
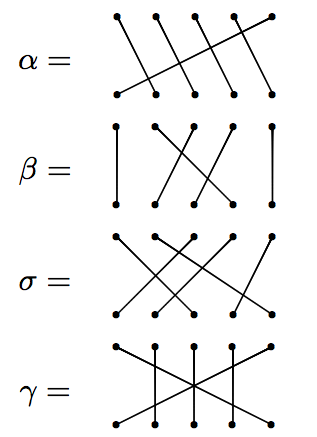
Permutation diagrams (continued)
Let's try multiplying.
Example
Let $\alpha$ and $\beta$ be as on previous slide. Then

But on the other hand
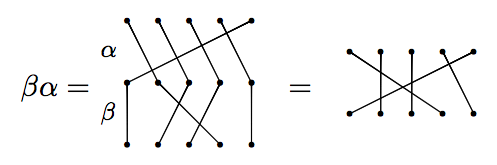
We see that products of permutations do not necessarily commute (order matters).
Permutation diagrams (continued)
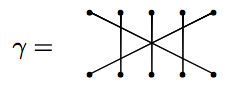
However, sometimes permutations do commute.
Example
Let $\beta$ and $\gamma$ be as before. Then

Notice that these result in the same diagram. So, $\beta$ and $\gamma$ commute.
Some comments
- Order matters, but not always.
- A diagram that swaps precisely two numbers is called a transposition.
- "Disjoint" transpositions commute.
- $S_n$ is generated by the transpositions. That is, every permutation can be written as a product of some sequence of transpositions. (In fact, we only need the adjacent transpositions: $i$ swaps with $i+1$).
The mind swaps as a diagram
If we let $a=1$, $h=2$, $l=3$, $p=4$, $b=5$, $e=6$, and $w=7$, $f=8$, and $z=9$, then the mind swaps from Futurama can be depicted as:
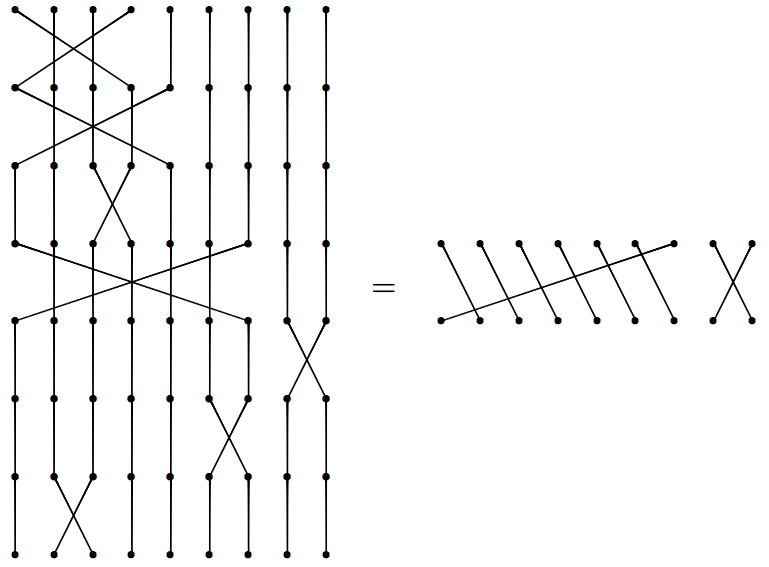
Rephrasing the problem
The problem can be restated as:
Can we multiply a permutation by a sequence of transpositions that we have not yet used to obtain the identity permutation?
It turns out that, in general, the answer is yes, but to pull this off, we need to add in two more people that have not used the machine.
Cycle notation
Before describing the solution, we need to introduce a more efficient way of encoding our permutations. One such method is called cycle notation.
Example
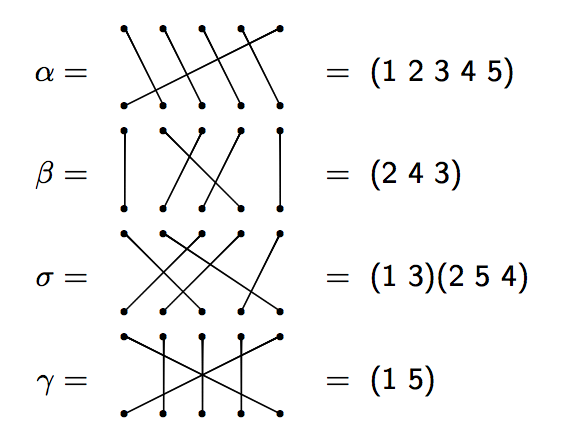
Cycle notation (continued)
Let's try multiplying using cycle notation. Note: We will multiply right to left (like function composition).
Example
Consider $\alpha, \beta$, and $\gamma$ in $S_{5}$ as in the previous examples. Then
\[\alpha \beta=(1\quad 2\quad 3\quad 4\quad 5)(2\quad 4\quad 3)=(1\quad 2\quad 5).\]
and
\[\gamma\beta =(2\quad 4\quad 3)(1\quad 5)=(1\quad 5)(2\quad 4\quad 3).\]
We saw earlier that $\beta$ and $\gamma$ commute with each other, which is why it looks like nothing happened in the second example.
Some more comments
- In cycle notation, the Futurama permutation is $(8\quad 9)(1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7)$.
- The interpretation of a cycle $(\ldots\quad i\quad j\quad \ldots)$ is that the body numbered $i$ passes its mind to the body $j$, etc.
- Transpositions are of the form $(i\quad j)$, which means that $i$ and $j$ swap minds.
- "Disjoint" cycles (including transpositions) commute.
- If we can figure out how to "fix" one cycle at a time, then we can likely fix them all.
Fixing a single 7-cycle
Consider just the 7-cycle $(1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7)$. Introduce two new bodies that have not had their minds swapped with anyone else, say $x$ and $y$. To return all minds of 1-7 back to their rightful owner, multiply the cycle (on the left) by the following sequence of transpositions:
\[(x\quad 7)(y\quad 1)(y\quad 2)(y\quad 3)(y\quad 4)(y\quad 5)(y\quad 6)(y\quad 7)(x\quad 1)\]
Let's verify that this actually works! First, notice that all of these transpositions are distinct and since $x$ and $y$ are new, we never used any of the transpositions to obtain our original scrambling of minds.
\[(x\quad 7)(y\quad 1)(y\quad 2)(y\quad 3)(y\quad 4)(y\quad 5)(y\quad 6)(y\quad 7)(x\quad 1)(1\quad 2\quad 3\quad 4\quad 5\quad 6\quad 7)=???\]
Note: $x$ and $y$ now have their minds swapped with each other, but they never sat in the machine at the same time!
Fixing an arbitrary $k$-cycle
Consider the $k$-cycle $(1\quad 2\quad \ldots\quad k)$. How do we "fix" this cycle?
As before, introduce two new bodies that have not used the machine, say $x$ and $y$. To fix a $k$-cycle, multiply the cycle (on the left) by the following:
\[(x\quad k)(y\quad 1)(y\quad 2)\cdots (y\quad k-1)(y\quad k)(x\quad 1)\]
Why does this work?!
- First observation: $(y\quad k)(x\quad 1)(1\quad 2\quad \ldots\quad k-1\quad k)=(1\quad 2\quad \ldots\quad k-1\quad y\quad k\quad x)$.
- Then $(y\quad k-1)$ puts the mind of $k-1$ back where it belongs.
- And then $(y\quad k-2)$ puts the mind of $k-2$ back where it belongs.
- We continue this way and in the second to last step, $(y\quad 1)$ puts the mind of 1 back where it belongs.
- And finally, we finish by swapping $x$ and $k$.
- We now have $x$ and $y$ with their minds swapped (but they never sat in the machine at the same time).
Fixing products of disjoint cycles
What do we do when we have multiple cycles to start with?
- Use $x$ and $y$ to fix each individual cycle.
- When doing this, $x$ and $y$ will sometimes be swapped.
- If the number of disjoint cycles is even, then we are done after we fix each individual cycle.
- If the number of disjoint cycles is odd, then after fixing each individual cycle, finish by swapping $x$ and $y$.
Closing remarks
Comments
- Our algorithm/proof is a special case of the one given on the board in the TV episode.
- Applying our algorithm to the arrangement of minds in Futurama requires 13 moves.
- But since Fry and Zoiberg only swapped with each other and since there is only one other cycle, we could use Fry and Zoiberg as $x$ and $y$, respectively in our algorithm. This only requires 9 moves.
Okay, that's it. Thank you!
Any questions?
These slides were made using deck.js and MathJax.
←
→
/
#