2. Blogging
3. Jul 14, 2014

My colleague Nandor Sieben and I recently submitted for publication a paper titled “Impartial achievement and avoidance games for generating finite groups.” The current arXiv version of the article is located here. My typical pure mathematics research interests are in the combinatorics of Coxeter groups and their associated algebras, so while I have a background in group theory and combinatorics, this was my first research experience in combinatorial game theory. In fact, prior to working on this project, I knew next to nothing about the subject. In the year and a half we worked on the project, I learned a tremendous amount of new material, which was a lot of fun. It was exciting to branch out and try something new.

Here is the abstract for the paper:

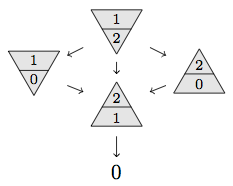
We study two impartial games introduced by Anderson and Harary and further developed by Barnes. Both games are played by two players who alternately select previously unselected elements of a finite group. The first player who builds a generating set from the jointly selected elements wins the first game. The first player who cannot select an element without building a generating set loses the second game. After the development of some general results, we determine the nim-numbers of these games for abelian and dihedral groups. We also present some conjectures based on computer calculations. Our main computational and theoretical tool is the structure diagram of a game, which is a type of identification digraph of the game digraph that is compatible with the nim-numbers of the positions. Structure diagrams also provide simple yet intuitive visualizations of these games that capture the complexity of the positions.

The fundamental problem in the theory of impartial combinatorial games is the determination of the nim-number of the game. This allows for the calculation of the nim-numbers of game sums and the determination of the outcome of the games. The major aim of this paper is the development of some theoretical tools that allow the calculation of the nim-numbers of the achievement and avoidance games for a variety of familiar groups. In the paper, we introduce the structure diagram of a game, which is an identification digraph of the game digraph that is compatible with the nim-numbers of the positions. Structure diagrams also provide simple but intuitive visualizations of these games that capture the complexity of the positions. By making further identifications, we obtain the simplified structure diagram of a game, which is our main computational and theoretical tool in the paper.

We developed a software package that computes the simplified structure digraph of the achievement and avoidance games. We used GAP to get the maximal subgroups and the rest of the computation is implemented in C++. The software is efficient enough to allow us to compute the nim-numbers for the smallest 100,000 groups, which includes all groups up to size 511. The result is available on our companion web page.

In April of 2013, I gave two talks at the University of Nebraska at Omaha that introduce the two games that this paper is about, but did not elaborate on the nim-number aspect. I summarized those talks in this blog post.